In a Nutshell: Parabola Forms
part of the In a Nutshell series on Adrian’s Study Club
Factored form y=a(x-x_1)(x-x_2)
Given:
- 2 x-ints
- One other point `P(x,y)
Vertex Form y=a(x-h)^2 + k
Given:
- Vertex
V(h,k) P(x, y)
General Form y=ax^2 + bx + c
Given:
- 3 points
OR
- 2 points
- y-int where
y-int = c
OR
- Axis of symmetry `x=-(b/2a)
- 2 other points
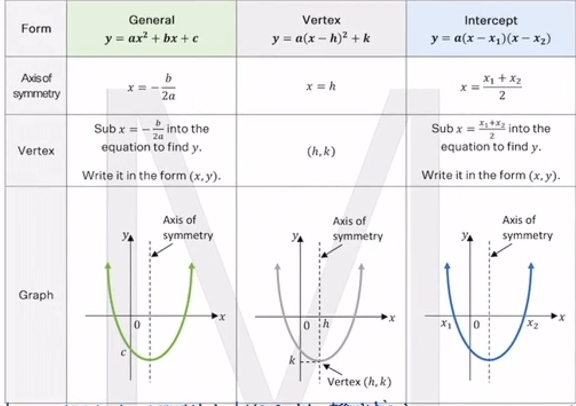
| Form | General y = ax^-2 + bx + c | Vertex y =a (x-h)^2 + k | Intercept y=(x-x_1)(x-x_2) |
|---|---|---|---|
| Axis of symmetry | x = -(b/2a) | x = h | x=((x_1 + x_2)/2) |
| Vertex | Sub x = -(b/2a) into the equation to find y. | (h, k) | Sub x=((x_1 + x_2)/2) into the equation to find y. |
| Form | Vertical Translation y = ax^2 + c | Horizontal translation y=a(x-h)^2 |
|---|---|---|
| Axis of symmetry | x=0 (y-axis) | x=h |
| Vertex | V(O,c) | V(h,0) |